- 浏览: 94485 次
- 性别:

- 来自: 宁德
-

最新评论
-
oudoud:
非常不错,没见收藏按钮
240多个jQuery插件 -
idning:
ding
生日悖论 -
java之渴望:
<%@ page contentType="& ...
将网页数据导出到Excel(以最简单的方式呈现) -
zhoujiabin810812:
简介明了!
黑莓(BlackBerry)是什么 -
WiseNeuron:
谢谢。标记一下
240多个jQuery插件
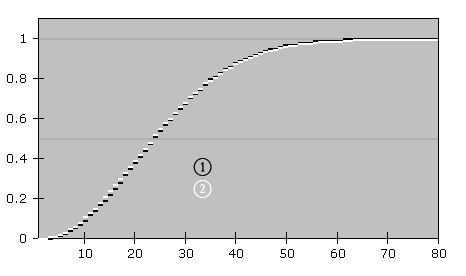
生日悖论是指,如果一个房间裡有23个或23个以上的人,那么至少有两个人的生日相同的概率要大于50%。这就意味着在一个典型的标准小学班级(30人)中,存在两人生日相同的可能性更高。对于60或者更多的人,这种概率要大于99%。从引起逻辑矛盾的角度来说生日悖论并不是一种悖论,从这个数学事实与一般直觉相抵触的意义上,它才称得上是一个悖论。大多数人会认为,23人中有2人生日相同的概率应该远远小于50%。计算与此相关的概率被称为生日问题, 在这个问题之后的数学理论已被用于设计著名的密码攻击方法:生日攻击。
目录 |
<script type="text/javascript"></script>
对此悖论的解释
理解生日悖论的关键在于领会相同生日的搭配可以是相当多的。如在前面所提到的例子,23个人可以产生C(23,2)= 23 × 22/2 = 253 种不同的搭配,而这每一种搭配都有成功相等的可能。从这样的角度看,在253种搭配中产生一对成功的配对也并不是那样的不可思议。
换一个角度,如果你进入了一个有着22个人的房间,房间裡的人中会和你有相同生日的概率便不是50:50了,而是变得非常低。原因是这时候只能产生22种不同的搭配。生日问题实际上是在问任何23个人中会有两人生日相同的概率是多少。
概率估计
假設有 n 個人在同一房間內,如果要計算有兩個人在同一日出生的機率,在不考慮特殊因素的前提下,例如閏年、雙胞胎,假設一年365日出生概率是平均分佈的(現實生活中,出生機率不是平均分佈的)。
計算機率的方法是,首先找出p(n)表示 n 個人中,每個人的生日日期都不同的概率。假如n > 365,根據鴿巢原理其概率為0,假设 n ≤ 365,则概率为
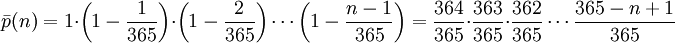
因为第二个人不能跟第一个人有相同的生日(概率是364/365), 第三个人不能跟前两个人生日相同(概率为363/365),依此类推。用阶乘可以写成如下形式

p(n)表示 n个人中至少2人生日相同的概率

n≤365,根据鸽巢原理, n大于365时概率为1。
当 n=23发生的概率大约是0.507。其他数字的概率用上面的算法可以近似的得出来:
| 10 | 12% |
| 20 | 41% |
| 30 | 70% |
| 50 | 97% |
| 100 | 99.99996% |
| 200 | 99.9999999999999999999999999998% |
| 300 | 1 − (7 × 10−73) |
| 350 | 1 − (3 × 10−131) |
| ≥366 | 100% |
注意所有人都是随机选出的:作为对比,q(n)表示房间中 n个其他人中与特定人(比如你)有相同生日的概率:

当n = 22时概率只有大约0.059,约高于十七分之一。如果n个人中有50%概率存在某人跟你有相同生日, n至少要达到253 。注意这个数字大大高于365/2 = 182.5: 究其原因是因为房间内可能有些人生日相同。
数学论证(非数字方法)
在 Paul Halmos 的自传中,他认为生日悖论仅通过数值上的计算来解释是一种悲哀。为此,Paul Halmos给出了一种概念数学方法的解释,下面就是这种方法(尽管这个方法包含一定的误差)。 乘积
 }-
}- 等于 1-p(n), 因此我们关注第一个n,使得乘积小于1/2,这样我们得到
![\sqrt[n-1]{\prod_{k=1}^{n-1}\left(1-{k \over 365}\right)}
<{1 \over n-1}\sum_{k=1}^{n-1}\left(1-{k \over 365}\right)](http://upload.wikimedia.org/math/3/b/2/3b292143b2a05a91f95e6e2ad86d5769.png) }-
}- 由平均数不等式得:

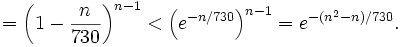 }-
}- (我们首先利用已知的1到n-1所有整数和等于 n(n-1)/2, 然后利用不等式不等式 1-x < e−x.) 如果仅当

最后一个表达式的值会小于0.5。 其中"loge"表示自然对数。这个数略微小于506,运气稍微好一点点就可以达到506,等于n2-n,我们就得到n=23。
在推导中,Halmos写道:
这个推导是基于一些数学系学生必须掌握的重要工具。生日问题曾经是一个绝妙的例子,用来演示纯思维是如何胜过机械计算:一两分钟就可以写出这些不等式,而乘法运算则需要更多时间,并更易出错,无论使用的工具是一只铅笔还是一台老式电脑。计算器不能提供的是理解力,或数学才能,或产生更高级、普适化理论的坚实基础。[1]。
然而Halmos的推导只显示至少需要23人保证平等机会下的生日匹配;因为我们不知道给出的不等式有多清晰,因此n=22能够正切的可能也无法确定。
泛化和逼近
生日悖论可以推广一下:假设有n 个,每一个人都随机地从1和特定的N个数中选择出来一个数(N可能是365或者其他的大于0的整数)。
p(n)表示有两个人选择了同样的数字,这个概率有多大?
下面的逼近公式可以回答这个问题

N=365的结果
泛化
下面我们泛化生日问题: 给定从符合离散均匀分布的区间[1,d]随机取出n个整数, 至少2个数字相同的概率p(n;d) 有多大?
类似的结果可以根据上面的推导得出。
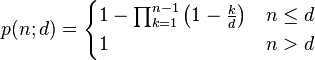


 }-
}- 反算问题
反算问题可能是:
对这个问题有如下逼近公式:
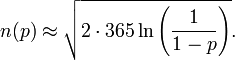
举例
| 逼近 | 估计N :=365 | |||||
| p | n 推广 | n <N :=365 | n↓ | p(n↓) | n↑ | p(n↑) |
|
0.01
|
0.14178 √N |
2.70864
|
2 | 0.00274 | 3 |
0.00820
|
| 0.05 | 0.32029 √N | 6.11916 | 6 | 0.04046 | 7 | 0.05624 |
|
0.1
|
0.45904 √N |
8.77002
|
8 | 0.07434 | 9 |
0.09462
|
|
0.2
|
0.66805 √N |
12.76302
|
12 | 0.16702 | 13 |
0.19441
|
| 0.3 | 0.84460 √N | 16.13607 | 16 | 0.28360 | 17 | 0.31501 |
| 0.5 | 1.17741 √N | 22.49439 | 22 | 0.47570 | 23 | 0.50730 |
| 0.7 | 1.55176 √N | 29.64625 | 29 | 0.68097 | 30 | 0.70632 |
| 0.8 | 1.79412 √N | 34.27666 | 34 | 0.79532 | 35 | 0.81438 |
| 0.9 | 2.14597 √N | 40.99862 | 40 | 0.89123 | 41 | 0.90315 |
| 0.95 | 2.44775 √N | 46.76414 | 46 | 0.94825 | 47 | 0.95477 |
|
0.99
|
3.03485 √N |
57.98081
|
57 |
0.99012
|
58 | 0.99166 |
注意:某些值被着色,说明逼近 不 总是正确。
经验性测试
生日悖论可以用计算机代码经验性模拟
days := 365; numPeople := 1; prob := 0.0; while prob < 0.5 begin numPeople := numPeople + 1; prob := 1 - ((1-prob) * (days-(numPeople-1)) / days); print "Number of people: " + numPeople; print "Prob. of same birthday: " + prob; end;
应用
生日悖论普遍的应用于检测哈希函数:N-位长度的哈希表可能发生碰撞测试次数不是2N次而是只有2N/2次。这一结论被应用到破解密码学散列函数的生日攻击中。
生日问题所隐含的理论已经在[Schnabel 1938]名字叫做capture-recapture的统计试验得到应用,来估计湖里鱼的数量。
不平衡概率
就像上面提到的,真实世界的人口出生日期并不是平均分布的。这种非均衡生日概率问题也已经被解决。[Klamkin 1967]
近似匹配
此问题另外一个范化就是求得要在随机选取多少人中才能找到2个人生日相同,相差1天,2天等的概率大于50% 。这是个更难的问题需要用到容斥原理。结果(假设生日依然按照平均分布)正像在标准生日问题中那样令人吃惊:
| 0 | 23 |
| 1 | 14 |
| 2 | 11 |
| 3 | 9 |
| 4 | 8 |
| 5 | 7 |
| 7 | 6 |
只需要随机抽取6个人,找到两个人生日相差一周以内的概率就会超过50%。
参考
- Zoe Emily Schnabel: "The estimation of the total fish population of a lake"(某湖中鱼类总量估计), 美国数学月刊 45 (1938年), 348-352页
- M. Klamkin,D. Newman: "Extensions of the birthday surprise"(生日惊喜的扩充), Journal of Combinatorial Theory 3 (1967年),279-282页。
- D. Blom: "a birthday problem"生日问题, 美国数学月刊 80 (1973年),1141-1142页。这一论文证明了当生日按照平均分布,两个生日相同的概率最小。
发表评论
-
你想知道您的那个端口号被那个程序占用了吗?
2009-09-14 18:24 2521以下文章主要以80端口号为例,如果想知道其他的端口号也可以使用 ... -
在电话接入时处理音频播放
2009-08-11 00:56 953通话是手机最重要的功能,手机来电会抑制正在运行的MIDlet运 ... -
单向陷门函数
2009-08-11 00:55 2637单向陷门函数(One-way Trapdoor Functio ... -
RSA加密算法
2009-08-11 00:54 26121. 密钥的产生① 选两个 ... -
数据加密标准DES
2009-08-11 00:54 1420数据加密标准DES 数据加密算法(Data Encryp ... -
Java做一个最简单的Socket通话程序
2009-08-11 00:53 1078Java中的网络编程是一个很重要的部分,也是其编程优越性的地方 ... -
C/S模式中的远程方法调用
2009-08-11 00:52 2006摘要 基于C/S设计模式, ... -
Java加密和数字签名编程快速入门
2009-08-11 00:51 646文/jwsh1984 本文主要谈一下密码学中的加密和 ... -
Vigenere密码与Playfair密码 收
2009-08-11 00:50 3919维吉尼亚(vigenere)密码,美国南北战争期间联军广泛 ... -
java实现DES加密算法
2009-08-11 00:49 2379一、java实现DES加密算法 为了实现一对密钥对整个项目所有 ... -
DES算法理论
2009-08-11 00:48 1381DES算法理论 本世纪五� ... -
欧拉函数
2009-08-11 00:47 1551当n为1至1000的整数时的值 ... -
悖论概念
2009-08-11 00:47 752其定义可以这样表述:由一个被承认是真的命题为前提,设为B,进行 ... -
TCP/IP端口基础常识大全
2009-08-11 00:44 743端口可分为3大类: 1) 公认端口(Well Known Po ... -
嵌入式处理器的基本概念
2009-08-11 00:42 1036嵌入式系统的核心部件是各种类型的嵌入式处理器,目前全世界嵌入式 ... -
嵌入式实时操作系统的现状和未来
2009-08-11 00:42 1195内容摘要:从RTOS(嵌入式实时操作系统)发展的历史、RTOS ... -
网络编程--WININET
2009-08-11 00:40 1549一个Internet客户端程序的目的是通过Interne ... -
Mod运算
2009-08-11 00:37 1634模p运算 给定一个正整数p,任意一个整数n,一定存在等式 ... -
欧拉定理 (数论)
2009-08-11 00:36 1602在数论中欧拉定理(也称费马-欧拉定理或欧拉函数定理: 若m,a ... -
数字签名和加密
2009-08-11 00:36 3816具体步骤如下。Alice与Bob互换公钥。Alice用自己的私 ...








相关推荐
问题:生日悖论分析。生日悖论指如果一个房间里有23人或以上,那么至少有两个人生日相同的概率大于50%。编写程序,输出在不同随机样本数量下,23个人中至少有两个人生日相同的概率。 import random 构建一个函数,...
一个房间有23个人,会有两个人生日相同吗?答案是有50%的概率。这就是所谓的生日问题birthday problem)或生日悖论(birthday paradox)。本文回答的问题是,当人数众多时,生日相同的概率达到50%,有多少人。
绘制生日悖论图
可以
生日悖论的互动演示 要求 需要来安装依赖项并通过npm运行脚本。 可用命令 命令 描述 npm install 安装项目依赖项 npm start 构建项目并打开运行Web服务器的项目 npm run build 使用生产设置(最小化,丑化等)...
从引起逻辑矛盾的角度来说生日悖论并不是一种悖论,从这个数学事实与一般直觉相抵触的意义上,它才称得上是一个悖论。大多数人会认为,23人中有2人生日相同的概率应该远远小于50%。计算与此相关的概率被称为生日问题...
目录 · · · · · · 出版者的话 专家指导委员会 译者序 前言 第一部分 基础知识 引言 第1章 算法在计算中的作用 1.1 算法 1.2 作为一种技术的算法 ...5.4.1 生日悖论 5.4.2 球与盒子 5.4.3 序列
5.4.1 生日悖论 5.4.2 球与盒子 5.4.3 序列 …… 第二部分 排序和统计学 引言 第6章 堆排序 第7章 快速排序 第8章 线性时间排序 第9章 中位数和顺序统计学 第三部分 数据结构 第10章 基本数据结构 第11章 散列表 第...
5.4.1 生日悖论 5.4.2 球与盒子 5.4.3 序列 …… 第二部分 排序和统计学 引言 第6章 堆排序 第7章 快速排序 第8章 线性时间排序 第9章 中位数和顺序统计学 第三部分 数据结构 第10章 基本数据结构 第11章 散列表 第...
5.4.1 生日悖论 5.4.2 球与盒子 5.4.3 序列 …… 第二部分 排序和统计学 引言 第6章 堆排序 第7章 快速排序 第8章 线性时间排序 第9章 中位数和顺序统计学 第三部分 数据结构 第10章 基本数据结构 第11章 散列表 第...
1.什么是哈希碰撞?产生哈希碰撞的原因是什么?如何避免? 两个不同的输入,经过哈希算法后,得到了同样的哈希值,就叫做哈希碰撞。由于通常的哈希算法中,哈希值的空间远小于输入的... 生日悖论:如果一个房间里
内容简介:在有关算法的书中,有一些叙述非常严谨,但不够全面,另一些涉及了大量的题材...5.2 指示器随机变量 5.3 随机算法 5.4 概率分析和指示器随机变量的进一步使用 5.4.1 生日悖论 5.4.2 球与盒子 5.4.3 序列 ……
5.4.1 生日悖论 5.4.2 球与盒子 5.4.3 序列 5.4.4 在线雇用问题 第二部分 排序和顺序统计学 引言 第6章 堆排序 6.1 堆 6.2 保持堆的性质 6.3 建堆 6.4 堆排序算法 6.5 优先级队列 第7章 ...
5.4.1 生日悖论 5.4.2 球与盒子 5.4.3 序列 5.4.4 在线雇用问题 第二部分 排序和顺序统计学 引言 第6章 堆排序 6.1 堆 6.2 保持堆的性质 6.3 建堆 6.4 堆排序算法 6.5 优先级队列 第7章 ...
关于加密 ...单向散列函数单向哈希函数(或称消息摘要,哈希函数,杂凑函数) 函数性质 函数类型:MD4,MD5,SHA-1,SHA-256,SHA-384,SHA-512,SHA-3等 ...生日攻击的原理来自生日悖论,也就是利用了“任意散列值一
在重复抽奖过程中某些数字会重复的概率比较高(类似于所谓的“生日悖论”中的概率,参见http://en.wikipedia.org/wiki/Birthday_problem)。 对于 Windows 10,下载最新版本的 zip 文件(绿色下载按钮),其中包含...
A 部分通常涉及创建类似于标准 UNIX 程序的程序,而 B 部分总是涉及扩展的功能,是一个简单的类 UNIX 操作系统,专为教育目的而设计.p1甲部一个演示生日悖论的简单程序。 这是一个热身项目,旨在刷新学生的 C 编程...
变量和表达式:设计自己的计算器循环和条件:跳房子列表,元组和条件句:让我们去旅行无处不在的抽象:手机中的应用程序数糖果:拥护者生日悖论:找到双胞胎Google翻译:可以使用任何语言货币换算器:计算您的国外...
1)生日悖论之二 127 2〕)升级概率问题 128 3)碰撞概率…,… 128 4)布丰投针问题,…,,… …128 )概率组合示例….129 13.排列组合问题 130 GoogLe+@http://dwz.cn/fada5 CsdN@http://dwz.cn/as2ik 1)...